
ответ и код
30
def f(x,a1,a2):
P = 10 <= x <= 20
Q = 25 <= x <= 55
A = a1 <= x <= a2
return A <= (P or Q)
d = []
for x in 10, 20, 25, 55:
d.append(x)
d.append(x-0.01)
d.append(x+0.01)
z = []
for a1 in d:
for a2 in d:
if a2>=a1 and all(f(x,a1,a2) for x in d):
z.append(a2-a1)
print(max(z))

ответ и код
1331.9899999999998 ==> 1332
def f(x,a1,a2):
P = 1023 <= x <= 2148
Q = 1362 <= x <= 3898
R = 1813 <= x <= 2566
A = a1 <= x <= a2
return (not((Q)<=(P or R)))<=((not A)<=(not Q))
d = []
for x in 1023, 2148, 1362, 3898, 1813, 2566:
d.append(x)
d.append(x-0.01)
d.append(x+0.01)
z = []
for a1 in d:
for a2 in d:
if a2>=a1 and all(f(x,a1,a2) for x in d):
z.append(a2-a1)
print(min(z))
ответ и код
85
def f(x,a1,a2):
P = 55 <= x <= 80
Q = 20 <= x <= 105
A = a1 <= x <= a2
return (Q)<= ((P==Q)or((not P)<=(A)))
d = []
for x in 55, 80, 20, 105:
d.append(x)
d.append(x-0.01)
d.append(x+0.01)
z = []
for a1 in d:
for a2 in d:
if a2>=a1 and all(f(x,a1,a2) for x in d):
z.append(a2-a1)
print(min(z))
ответ и код
19.990000000000002 ==> 20
def f(x,a1,a2):
P = 15 <= x <= 40
Q = 35 <= x <= 60
A = a1 <= x <= a2
return not (((not Q)or (P)) and (A)) #not - так как нужны 0 значения
d = []
for x in 15, 40, 35, 60:
d.append(x)
d.append(x-0.01)
d.append(x+0.01)
z = []
for a1 in d:
for a2 in d:
if a2>=a1 and all(f(x,a1,a2) for x in d):
z.append(a2-a1)
print(max(z))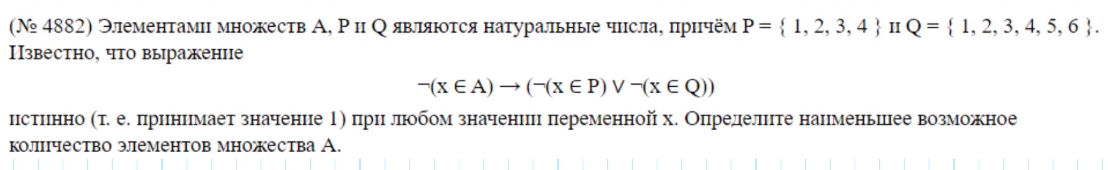
ответ и код
4
def f(x,a):
P = x in {1,2,3,4}
Q = x in {1,2,3,4,5,6}
A = x in a
return (not A) <= ((not P) or (not Q))
a = set()
for x in range(1,100):
if f(x,a) == 0:
a.add(x)
print(len(a))

ответ и код
90
import math
def f(x,a):
P = x in {2,4,9,10,15}
Q = x in {3,8,9,10,20}
A = x in a
return (not(P==A))<=(Q == A)
a = set()
for x in range(1,100):
if f(x,a) == 0:
a.add(x)
print(math.prod(a))
ответ и код
18
def f(x,a):
P = x in {x for x in range(2,22,2)} #можно и так {2,4,6,8,10,12,14,16,18,20}
Q = x in {x for x in range(5,55,5)} #можно и так {5,10,15,20,25,30,35,40,45,50}
A = x in a
return (A <= P) or ((not Q)<= (not A))
a = set(range(1,100))
for x in range(1,100):
if f(x,a) == 0:
a.remove(x)
print(len(a))
конспект
Статья в ВК: https://vk.com/@-205546952-zadanie-15-konspekt-programma-ch2
avatar
Курс
Годовой курс
Задание 15 (программа)
Конспект к занятию №2
Задача № 1 (363)
На числовой прямой даны два отрезка: P=[10,20] и Q=[25,55]. Определите наибольшую возможную длину отрезка A, при котором формула
(x ∈ A) → ((x ∈ P) ∨ (x ∈ Q))
тождественно истинна, то есть принимает значение 1 при любом значении переменной х.
Ссылка на видео-разбор с таймингом: https://vk.com/video-205546952_456241198?t=1m40s
При решении задач с отрезками есть три проблемы. Первая и основная проблема – неизвестно что является отрезком, как его задавать, как его перебирать. Вторая проблема – в отличие от остальных задач в подобных этим, нужно проверять не только целые или натуральные, но также и дробные значения. Т. е. переменная «х» в этих задачах может принимать не только целые значение, но и любые дробные между ними.
И третья сложность состоит в том, что неизвестный отрезок может являться полуинтервалом или интервалом, т.е. иметь обе или одну из границ не входящих в указанный диапазон – выколотые точки.
Для понимания, как решать эти проблемы разберем два важных момента, следующих из аналитического решения подобных задач. Воспользуемся рисунком числовой прямой. На этой прямой есть два числа, обозначающих его начало и конец. Это касается отрезка P, отрезка Q, и то же самое касается и отрезка A. Нужно перебрать разные варианты начала и конца этого отрезка.
Первый вопрос, какими способами можно перебрать все варианты значений начала и конца? Первый способ – перебрать все возможные варианты отрезков на числовой прямой, начиная с условной единицы и заканчивая удаленной от нее на определенную величину конечной точки, рассмотреть отрезки разной длины. Но это может занять довольно много времени, потому что разных пар, разных комбинаций будет много.
Второй способ. Отрезок А, который мы ищем, минимальный, или максимальный, имеет концы, которые в любом случае опираются на уже известные точки. Вспомним аналитическое решение подобных задач. Во всех случаях у искомых отрезков концы соответствовали концам уже известных отрезков. Отсюда мы можем сделать вывод, что для обычных типовых задач, в которых требуется найти минимальный отрезок или максимальный отрезок, нет смысла перебирать все возможные отрезки. Достаточно проверить только известные точки данных нам отрезков
Второй вопрос связан с первым. Какие точки, сколько точек на числовой прямой нам надо проверить, чтобы убедиться, что выражение действительно будет тождественно истинным, что действительно найден такой отрезок А, что для любой точки «х», как целой, так и дробной, выражение действительно выполняется. Может показаться, что для этого нужно перебрать очень много чисел, но фактически достаточно очень небольшого количества для того, чтобы убедиться в истинности выражения. Во-первых, это будут опять те же самые концы отрезков, в них действительно выражение имеет значение истины. И во-вторых, достаточно проверить точки, которые, находятся непосредственной от них близости, отличаясь на очень малую величину (0,1…0,01). Если в этих точках, выражение будет равно единице, значит, можно гарантировать, что оно будет равно единице на всём исследуемом диапазоне, потому что, для всего этого диапазона положение всех отрезков одинаковое. Следовательно, если в этих двух точках выполняются условия, значит они автоматически выполняются на всем исследуемом диапазоне. Т.е. не нужно проверять не огромное количество точек на всей числовой прямой, а достаточно проверить по две точки в каждом из диапазонов прямой, которые получились разбиением концами заданных отрезков.
Решение
Создадим функцию, которая будет проверять значение заданного логического выражения. Функция получает число «x» и значения концов отрезка А, «а1» и «а2». « а1» — это начало нашего отрезка, «а2» — это конец нашего отрезка. Функция будет возвращать значение заданного выражения. Создадим список, в котором будут все точки, которые нужно проверить, чтобы выражение было тождественно истинным и которые могут оказаться концами отрезка А.
Сначала рассмотрим длинную запись.
Заполним список d путем перебора чисел, являющихся концами отрезка 10, 20, 25, 55. В него попадут, во-первых, число x, во-вторых число немного меньше, например, x - 0,01, и второе число немного больше x + 0,01. В итоге мы получили список чисел, которые с одной стороны являются концами известных отрезков Р и Q . С другой стороны это числа, которые находятся в какой-то ближайшей окрестности от них.
def f(x,a1,a2):
return (a1<=x<=a2) <= ((10<=x<=20) or (25<=x<=55))
d = []
for x in 10,20,25,55:
d.append(x)
d.append(x-0.01)
d.append(x+0.01)
print(d)
Так выглядит этот список:
[10, 9.99, 10.01, 20, 19.99, 20.01, 25, 24.99, 25.01, 55, 54.99, 55.01]
То есть, получены 12 точек, которые достаточно проверить для того, чтобы сказать выражение будет ли истинно выражение на всей числовой прямой.
В двойном цикле переберем все возможные пары «а1», «а2».
def f(x,a1,a2):
return (a1<=x<=a2) <= ((10<=x<=20) or (25<=x<=55))
d = []
for x in 10,20,25,55:
d.append(x)
d.append(x-0.01)
d.append(x+0.01)
for a1 in d:
for a2 in d:
if all(f(x,a1,a2)==1 for x in d):
print(a1,a2)
Результат работы программы:
10 10
10 9.99
10 10.01
10 20
...
20 10
20 9.99
20 10.01
20 20
20 19.99
Таким образом, мы перебираем разные варианты начала и конца отрезков. Но подобный перебор не является удачным решением, т.к. в нем могут оказаться случаи, когда первое число, являющееся началом отрезка больше, чем его конец. Чтобы избежать подобную проблему, дополним перебор условием «a2>=a1»
Далее для каждого варианта отрезка мы проверим, что функция равна единице во всех определенных ранее точках. Т. е. будем брать числа «x» из того же самого списка:
def f(x,a1,a2):
return (a1<=x<=a2) <= ((10<=x<=20) or (25<=x<=55))
d = []
for x in 10,20,25,55:
d.append(x)
d.append(x-0.01)
d.append(x+0.01)
for a1 in d:
for a2 in d:
if a2>=a1 and all(f(x,a1,a2)==1 for x in d):
print(a1,a2)
10 10
10 10.01
10 20
10 19.99
10.01 10.01
10.01 20
10.01 19.99
20 20
19.99 20
19.99 19.99
25 25
25 25.01
25 55
25 54.99
25.01 25.01
25.01 55
25.01 54.99
55 55
54.99 55
54.99 54.99
Обратим внимание, что все полученные отрезки, нам подходят.
В задании требуется указать наибольшую длину подходящего отрезка. Длину любого отрезка можно получить вычитанием начальной его точки из конечной точки.
def f(x,a1,a2):
return (a1<=x<=a2) <= ((10<=x<=20) or (25<=x<=55))
d = []
for x in 10,20,25,55:
d.append(x)
d.append(x-0.01)
d.append(x+0.01)
for a1 in d:
for a2 in d:
if a2>=a1 and all(f(x,a1,a2)==1 for x in d):
print(a2-a1)
Результаты работы программы список длин подходящих отрезков:
0
0.009999999999999787
10
9.989999999999998
0.0
9.99
9.979999999999999
0
0.010000000000001563
0.0
0
0.010000000000001563
30
29.990000000000002
0.0
29.99
29.98
0
0.00999999999999801
0.0
Наибольшее число, которое мы здесь видим это 30. Это наибольшая длина из всех вариантов отрезков для которых функция всегда равна единице.
Сделаем этот вариант решения задачи более удобным. Будем искать максимум сразу одним числом. Для этого перед перебором создадим пустой список. И как только мы будем находить подходящий отрезок, будем его длину добавлять в этот список. В итоге мы получим список с длинами всех подходящих отрезков и в конце выведем максимальное значение этого списка.
Окончательный код для решения задачи:
def f(x,a1,a2):
return (a1<=x<=a2) <= ((10<=x<=20) or (25<=x<=55))
# составляем список чисел которые будут проверяться
d = []
for x in 10,20,25,55:
d.append(x)
d.append(x-0.01)
d.append(x+0.01)
# список для сохранения длин подходящих отрезков
m = []
for a1 in d:
for a2 in d:
if a2>=a1 and all(f(x,a1,a2)==1 for x in d):
m.append(a2-a1)
print(max(m))
Результат работы программы:
30
Ответ: 30
Задача №2 (6482)
На числовой прямой даны три отрезка: P = [1023; 2148], Q = [1362; 3898] и R = [1813; 2566]. Укажите наименьшую возможную длину такого отрезка A, что формула
(¬((x ∈ Q) → ((x ∈ P) ∨ (x ∈ R)))) → (¬(x ∈ A) → ¬(x ∈ Q))
тождественно истинна, то есть принимает значение 1 при любом значении переменной х?
Ссылка на видео-разбор с таймингом: https://vk.com/video-205546952_456241198?t=27m45s
Решение
Для сокращения записи в функции определяющей значение заданного выражения используем обозначения отрезков Р, Q, R задав их интервалы в виде числовых неравенств. P = 1023<=x<=2148, Q = 1362<=x<=3898, R = 1813<=x<=2566. Так же зададим отрезок А, обозначив его концы, как а1 и а2. Запишем само выражение аккуратно проставив все скобки для корректного выполнения последовательности логических операций.
Зададим список d из тех точек, которые достаточно проверить.
Напишем цикл для перебора возможных вариантов концов отрезка А, в котором будем проверять условие, что число, соответствующее правой границе (а2), больше а1 (левая граница) и для пар этих точек функция имеет значение истины. Будем добавлять длины подходящих отрезков в список m. В результате работы такой программы мы получим список различных вариантов длин отрезков, но так как по заданию нам нужно получить минимальную длину используем функцию min().
Обратим внимание, что полученный ответ представляет собой нецелое число с большой десятичной частью (1331.9899999999998). Это подтверждение того, что
отрезок А в данном случае не является отрезком, как таковым. Он представляет собой полуинтервал, т. е. отрезок, с «выколотыми» концами. При этом, если увеличивать точность приближения точек к точкам, обозначающим концы заданных отрезков число получаемое в ответе, оставаясь дробным, будет всё более приближаться к целому значению.
Код для решения задачи:
def f(x,a1,a2):
P = 1023<=x<=2148
Q = 1362<=x<=3898
R = 1813<=x<=2566
A = a1<=x<=a2
return (not(Q <= (P or R))) <= ((not A) <= (not Q))
# составляем список чисел которые будут проверяться
d = []
for x in 1023,2148,1362,3898,1813,2566:
d.append(x)
d.append(x-0.01)
d.append(x+0.01)
# список для сохранения длин подходящих отрезков
m = []
for a1 in d:
for a2 in d:
if a2>=a1 and all(f(x,a1,a2)==1 for x in d):
m.append(a2-a1)
print(min(m))
Результат работы программы:
1331.9899999999998
Для понимания как выглядит на числовой прямой отрезок разберем эту задачу методом аналитического решения.
Полученная в итоге упрощения импликация может быть прочитана как:
Если «x» принадлежит Q, то он должен принадлежать или P, или R, или A. По рисунку видно, что участок прямой от значения 2566 и 3898 не принадлежит ни Q, ни R, значит потенциально выражение здесь может иметь значение ложь.
Если рассмотреть концы этого участка, то окажется «выколотыми», то есть в точке со значение 2566 выражение будет иметь значение истины, а правее будет располагаться «ложь». Т.е. отрезок А является полуинтервалом до числа 3898, которое в него входит. Поэтому программа допускает небольшую погрешность, описывая максимально возможный промежуток, на котором значение выражения является ложным. Правильным ответом на задачу будет округленное по правилам математики число, при этом в программе можно использовать функцию round().
Ответ: 1332
Задача № 3 (4974)
На числовой прямой даны два отрезка: P = [55; 80], Q = [20; 105]. Найдите наименьшую возможную длину отрезка A, при котором формула
(x ∈ Q) → ( ((x ∈ P) ≡ (x ∈ Q)) ∨ (¬(x ∈ P) → (x ∈ A)) )
тождественно истинна, то есть принимает значение 1 при любых x.
Ссылка на видео-разбор с таймингом: https://vk.com/video-205546952_456241198?t=43m25s
Решение
На примере этой задачи разберём такое понятие, как глобальная область видимости переменных. В отличие от функций, которые мы создавали и использовали в предыдущих задачах, в описании функции к этому примеру мы не будем указывать в передаваемых значениях «а1» и «а2», потому что функция сама будет их брать из так называемой глобальной области видимости, являющейся областью памяти, в которой находятся созданные в задаче переменные, содержащие данные. Эти переменные можно использовать в любом месте кода задачи, в том числе и внутри функций.
Кроме этого сократим запись списка до одной строки.
Если запросить вывод списка из 4-х чисел, обозначающих границы заданных отрезков:
d = [x for x in (55,80,20,105) ]
print(d)
мы получим следующий результат, список их 4 чисел.:
[55, 80, 20, 105]
Но нам нужны не только эти числа, но и числа на 0,01 меньше, и на 0,1 больше. Для того внутри списка напишем еще один цикл для «у», в котором будем перебирать значение x+ 0,01 и значение x – 0,01. Из этих полученных чисел «у», будет формироваться необходимый для решения задачи список:
d = [y for x in (55,80,20,105) for y in (x,x+0.01,x-0.01)]
Результат:
[55, 55.01, 54.99, 80, 80.01, 79.99, 20, 20.01, 19.99, 105, 105.01, 104.99]
Полученный список будет использован для переменных а1 и а2 в переборе для проверки условия что число, соответствующее правой границе (а2), больше а1 (левая граница) и для пар этих точек функция возвращает
значение истины. При этом при вызове функции эти значения будут обновляться с каждым шагом цикла. Длины подходящих отрезков будем добавлять в созданный ранее пустой список m. Для получения ответа аналогично предыдущей задаче используем функцию min().
def f(x):
P = 55<=x<=80
Q = 20<=x<=105
# переменные а1 и а2 будут задаваться глобально
A = a1<=x<=a2
return Q <= ((P==Q) or ((not P) <= A))
# составляем список чисел у, которые будут проверяться
d = [y for x in (55,80,20,105) for y in (x,x+0.01,x-0.01)]
# пустой список m, в котором будем сохранять длины подходящих отрезков
m = []
for a1 in d:
for a2 in d:
if a2>=a1 and all(f(x)==1 for x in d):
m.append(a2-a1)
print(min(m))
Результат работы программы:
85
Ответ: 85
Задача № 4 (4597)
На числовой прямой даны два отрезка: P=[15,40] и Q=[35,60]. Найдите наибольшую возможную длину отрезка A, при котором формула
(¬(x∈Q)∨(x∈P))∧(x∈A)
тождественно ложна, то есть принимает значение 0 при любых x.
Ссылка на видео-разбор с таймингом: https://vk.com/video-205546952_456241198?t=55m5s
Решение
При решении этого номера закрепим приемы решения подобных задач, с которыми мы познакомились в предыдущем примере. Отличие этой задачи в том, что заданное выражение должно быть тождественно ложно и требуется найти максимальную возможную длину отрезка. Для этого в поиске подходящих значений в условии укажем, что f(x)=0, а в выводе результата применим функцию max()
def f(x):
P = 15<=x<=40
Q = 35<=x<=60
A = a1<=x<=a2
return (not Q or P) and A
d = [y for x in (15,40,35,60) for y in (x,x+0.01,x-0.01)]
m = []
for a1 in d:
for a2 in d:
# т.к. по условию высказывание должно быть тождественно ложно, f(x)==0
if a2>=a1 and all(f(x)==0 for x in d):
m.append(a2-a1)
print(max(m))
Результат работы программы:
19.990000000000002
Ответ: 20
Задача №5 (3477)
(Элементами множеств А, P и Q являются натуральные числа, причём P={1,2,3,4} и Q={1,2,3,4,5,6}. Известно, что выражение
¬(x∈A)→(¬(x∈P)∨¬(x∈Q))
истинно (т. е. принимает значение 1) при любом значении переменной х. Определите наименьшее возможное количество элементов множества A.
Ссылка на видео-разбор с таймингом https://vk.com/video-205546952_456241198?t=1h3m
Решение
Эта задача является задачей на множества, и особенностью её решение программой, является то, что результатом работы программы является результат исследования искомого множества. Рассмотрим принципы этого исследования.
Первым шагом зададим определим множество А с помощью функции set(), как пустое, не содержащие никаких элементов. Создадим функцию для заданного логического выражения, для удобства записав множества P, Q, А через переменную «х» в заданном в задаче множестве. Переберем значения x, в диапазоне чисел от 1 до 100. И выведем на экран те значения, в которых функция будет ложна.
a = set()
def f(x):
P = x in {1,2,3,4}
Q = x in {1,2,3,4,5,6}
A = x in a
return (not A) <= (not P or not Q)
for x in range(1,100):
if f(x)==0:
print(x)
Результат работы программы:
1
2
3
4
Таким образом мы определили, что при х =1, 2, 3, 4 наша логическая функция равна 0. Это произошло потому, что этих чисел нет как в двух заданных множествах, Р и Q, так и в являющемся пока пустым множестве А. Т.е., если эти числа добавить в множество А, функция будет истина. Выполним это действие с помощью метода добавления элементов в множество add(), и получим ответ, минимальное множество элементов А это 1, 2, 3, 4.
Код для решения задачи:
#создадим пустое множество А
a = set()
def f(x):
P = x in {1,2,3,4}
Q = x in {1,2,3,4,5,6}
A = x in a
return (not A) <= (not P or not Q)
#Переберем числа х от 1 до 100, если каком-то числе функция оказывается #равной нулю, следует это число добавить к множеству А
for x in range(1,100):
if f(x)==0:
a.add(x)
print(a)
Результат работы программы:
{1, 2, 3, 4}
Ответ: 4
Задача №6 (3477)
(С.А. Скопинцева) Элементами множества А являются натуральные числа. Известно, что выражение
¬((x ∈ {2, 4, 9, 10, 15}) ≡ (x ∈ A)) → ((x ∈ {3, 8, 9, 10, 20}) ≡ (x ∈ A))
истинно (т.е. принимает значение 1 при любом значении переменной х. Определите наименьшее возможное значение произведения элементов множества A.
Ссылка на видео-разбор с таймингом: https://vk.com/video-205546952_456241198?t=1h3m
Решение
Можно сказать, что в задаче речь идёт про наименьшее множество А, потому что элементы — это натуральные числа, а произведение натуральных чисел тем меньше, чем меньше входящих в него числа. Следовательно, решение этой задачи будет полностью аналогично решению предыдущего примера.
Код для решения задачи:
# создадим пустое множество А
a = set()
def f(x):
P = x in {2,4,9,10,15}
Q = x in {3,8,9,10,20}
A = x in a
return (not (P==A)) <= (Q==A)
# Переберем числа х от 1 до 100, если каком-то числе функция оказывается #равной нулю, следует это число добавить к множеству А
for x in range(1,100):
if f(x)==0:
a.add(x)
print(a)
Результат работы программы:
{9, 10}
Ответ: 90
Задание №7 (3434)
Элементами множеств А, P и Q являются натуральные числа, причём P={2, 4, 6, 8, 10, 12, 14, 16, 18, 20} и Q={5, 10, 15, 20, 25, 30, 35, 40, 45, 50}. Известно, что выражение
((x ∈ A) → (x ∈ P)) ∨ (¬(x ∈ Q) → ¬(x ∈ A))
истинно (т.е. принимает значение 1 при любом значении переменной х. Определите наибольшее возможное количество элементов в множестве A.
Ссылка на видео-разбор с таймингом: https://vk.com/video-205546952_456241198?t=1h9m25s
Решение
Подход в рассуждениях к решению данной задачи будет противоположным по отношению к ранее рассмотренным примерам задач с множествами, где требовалось определить минимальный размер множества.
Проделаем шаги аналогичные решению предыдущих задач, т.е. создадим множество А, задав его пустым. Создадим функцию для заданного логического выражения, для удобства записав множества P, Q, А через переменную «х» в заданном в задаче множестве. Найдем все числа x, для которых выражение ложное.
a = set()
def f(x):
P = x in {2,4,6,8,10,12,14,16,18,20}
Q = x in {5,10,15,20,25,30,35,40,45,50}
A = x in a
return (A <= P) or ((not Q) <= (not A))
for x in range(1,100):
if f(x)==0:
print(x)
Результат работы программы:
Запустим программу и обнаружим, чисел в которых функция ложна нет, вывод будет пустой. Т.е., если А – пустое множество, выражение везде равно единице, функция везде истина, и, это минимальное по размеру, пустое множество, соответствует тому, чтобы выражением было истинным, но, так как требуется определить наибольшее множество, в котором выражение истинно, нужно заполнить это множество числами и определить набор значений в котором функция f(х) =0.
Заполним множество числами от 1 до 100.
a = set(range(1,100))
def f(x):
P = x in {2,4,6,8,10,12,14,16,18,20}
Q = x in {5,10,15,20,25,30,35,40,45,50}
A = x in a
return (A <= P) or ((not Q) <= (not A))
for x in range(1,100):
if f(x)==0:
print(x)
Результат работы программы:
1
3
7
9
11
13
17
9
21
22
23
...
99
Теперь результат работы программы показывает, что значений «x», где функция равна 0, очень много. Это произошло потому, что в множестве А появились числа, для большинства из которых функция стала ложной. Заметим, что не все числа, которыми мы заполнили множество оказались в списке вывода. Например, в начале списка, числа идут не подряд. Значит, в этих числах, значение функции не равно нулю – исходное выражение имеет значение истины. Таким образом, для решения задачи требуется определить этот, не попавший в вывод набор чисел, соответствующий множеству всех чисел для которого выражение будет истинно. Можно вывести числа, в которых значение функции будет равно единице:
a = set(range(1,100))
def f(x):
P = x in {2,4,6,8,10,12,14,16,18,20}
Q = x in {5,10,15,20,25,30,35,40,45,50}
A = x in a
return (A <= P) or ((not Q) <= (not A))
for x in range(1,100):
if f(x)==1:
print(x)
Результат работы программы:
2
4
5
6
8
10
12
14
15
16
18
20
25
30
35
40
45
50
Очевидно, что для этих чисел f(x) =1, они все входят в множество А, и дают значение исходному выражению истина. Если же для получения ответа использовать f(x)=0, нам нужно, перебрав все элементы этого множества удалить из него те, которые дают ноль. И, затем, вывести оставшиеся в множестве А значения. Для удаления элементов множества можно использовать метод remove(). Полученные числа – наибольшее значений А, их количество является ответом на задачу.
Окончательный вариант для решения задачи:
# создадим множество А из некоторого количества натуральных чисел
a = set(range(1,100))
def f(x):
P = x in {2,4,6,8,10,12,14,16,18,20}
Q = x in {5,10,15,20,25,30,35,40,45,50}
A = x in a
return (A <= P) or ((not Q) <= (not A))
#если в числе х функция f(x)==0, то мы удаляем это число из множества А
for x in range(1,100):
if f(x)==0:
a.remove(x)
print(a)
Результат работы программы:
{2, 4, 5, 6, 8, 10, 12, 14, 15, 16, 18, 20, 25, 30, 35, 40, 45, 50}
Ответ: 18
Задание № 8(147)
(Е.В. Хламов) Пусть P – множество всех 8-битовых цепочек, начинающихся с 11, Q – множество всех 8-битовых цепочек, оканчивающихся на 0, а A – некоторое множество произвольных 8-битовых цепочек. Сколько элементов содержит минимальное множество A, при котором для любой 8-битовой цепочки x истинно выражение
¬(x∈A)→(¬(x∈P)∨(x∈Q))
Ссылка на видео-разбор с таймингом: https://vk.com/video-205546952_456241198?t=1h22m45s
Решение
В этой задаче множества состоят не из чисел, а из 8-битовых цепочек, т.е. последовательностей из нулей и единиц длины 8, в которой нули и единицы идут в разном порядке, в разных комбинациях. Будем рассматривать эти последовательности в виде строк. Для перебора всех комбинаций символов в этих строках (их будет 28 штук) будем использовать функцию product() из библиотеки itertools.
В функции для исходного выражения укажем, что множество P — это все строки(цепочки), которые начинаются на ‘11’, Q — все строки (цепочки), которые заканчиваются на ‘0’, A —произвольное множество 8-битовых цепочек. Т.к. в задаче требуется найти минимальное множество, зададим его пустым.
Проходим по всем восьмибитовым цепочкам и смотрим, если для какой-то из них выражение f (x)=0, эту цепочку необходимо добавить в множество А, заданное нами как, множество значений которого дают истину исходному выражению.
Так мы получим все подходящие цепочки в множество А. Это будет минимальное множество. Для ответа на задачу с помощью функции len() получим и выведем на экран его длину.
Код для решения задачи:
#подключим библиотеку itertools
from itertools import *
# создадим пустое множество А
a = set()
# сформируем множества Р и Q из элементов являющихся строками
# множество Р состоит из строк начинающихся на ‘11’
# множество Q состоит из строк оканчивающихся на ‘0’
def f(x):
P = x[0]+x[1] == '11'
Q = x[-1] == '0'
A = x in a
return (not A) <= (not P or Q)
# переберем 16-битовые цепочки
for x in product('01',repeat=8):
if f(x)==0:
#если функция данной цепочки равна 0, то мы добавляем ее к множеству
a.add(x)
print(len(a))
Результат работы программы:
32
Ответ: 32
ТЕСТ (закрепление отдельных моментов при написании кода)
ДОМАШНЯЯ РАБОТА (10 упражнений по 15 заданию ЕГЭ)