ЕГЭ-2 Построение таблиц истинности логических выражений

Задание 2 (часть 1). Конспект

Что такое логика?

Ссылка на видео-разбор с таймингом: https://vk.com/video-205546952_456241186?t=50s

Логика — это философская наука о формах и законах теоретического мышления, о связях этих форм и о допускаемых в процессе мышления ошибках, а также о способах их преодоления. Эта наука зародилась в Древней Греции. Хотя человечество элементы логики знало и раньше, но как полноценная дисциплина она выделилась именно в Древней Греции. Там оформились и зародились все основные положения этого предмета. Это называется классическая логика. Эта логика. в основном, направлена на словесную форму информации, то есть на работу с высказываниями, рассуждениями, поэтому в курсе информатики она не рассматривается.

Формирование алгебры логики

Ссылка на видео-разбор с таймингом: https://vk.com/video-205546952_456241186?t=3m15s

2,5 тысячи лет логика была частью философии, часть риторики. В 19 веке математиками того времени логика была выражена через математическую систему, т.е. записана формальным математическим языком (формализована). Языком цифр и математических операций. Таким образом сформировалась алгебра логики. Оказалось, что эту науку удобно применять в других отраслях, не только связанных с речью. Основной пик применения алгебры логики произошел при построении компьютеров, потому что все вычислительные устройства построены на логических элементах (транзисторах). Взаимодействие этих логических элементов, описывается языком математической логики. Поэтому алгебра логики — это основа для понимания работы компьютерной техники. Фреге, де Морган, Буль, Пирс являются основоположники алгебры логики.

Сравнение обычно алгебры и алгебры логики.

Ссылка на видео-разбор с таймингом: https://vk.com/video-205546952_456241186?t=7m5s

Основные логические операции.

Ссылка на видео-разбор с таймингом: https://vk.com/video-205546952_456241186?t=12m45s

Логических операций достаточно много. В ЕГЭ применяются в основном 5 операций. Мы разберем их в порядке приоритета, то есть в порядке их выполнения в логических выражениях.

Самый высокий приоритет у операции отрицания, т.е. в логических выражениях эта операция выполняется в первую очередь. Иначе эта операция называется инверсия. Она обозначается символами НЕ, ㄱ, Ā, not A (А — логическое высказывание). Если высказывание А истинно, то после инверсии оно станет ложным, и наоборот. В ЕГЭ она обозначается так ¬ А, если А равное нулю отрицание поменяет его значение на единицу, и, наоборот, если А было равно единице сделает его равным нулю.

Вторая по приоритету операция — называется конъюнкцией. Конъюнкцию обозначают символами И, ⴷ, &, А and В (А, В — простые логические высказывания). В ЕГЭ используется символ ⴷ.Эту логическую операцию выполняют минимум для двух простых высказываний. Она будет истинна только в том случае, когда все высказывания, для которых выполняется конъюнкция, истинны. Эту операцию называют логическим умножением поэтому, иногда для краткой записи используется запись А * B. Т.к. это операция логическое умножение её результат будет таким:

Следующая операция дизъюнкция — логическое сложение. Дизъюнкцию обозначают как ИЛИ, ∨, |, А or В. Эту логическую операцию выполняют минимум для двух простых логических высказываний. Она будет истинна в том случае, когда хотя бы одно из высказываний истинно. Эта операция работает аналогично арифметическому сложению.

Четвертая операция — импликация. Импликация или логическое следование. По смыслу приближена к высказываниям в форме «если… то…». Обозначается импликация А→В. Эта логическая операция, ставящая в соответствие двум высказываниям новое, являющееся ложным тогда и только тогда, когда первое высказывание (посылка) истинно, а второе (следствие) — ложно, называется импликацией (от лат. implicatio — сплетение, тесная связь).

Пятая используемая в ЕГЭ операция — эквиваленция. Эквивале́нция (или эквивале́нтность) — это логическое выражение, которое является истинным тогда, когда оба простых логических выражения имеют одинаковую истинность. Логическую эквивалентность А и В иногда обозначают как a≡b, А~В. Специфика союза “эквиваленция” состоит в том, что эквивалентное суждение признается истинным, когда оба входящие в ее состав исходные суждения имеют одинаковое значение истинности: либо они одновременно истинные, либо одновременно ложные.

Кроме перечисленных выше есть и другие логические операции. Например, операция XOR (исключающее или), являющаяся основой компьютерной техники; штрих Шеффера, черточка Пирса и другие.

Запись логических выражений в Python

Ссылка на видео-разбор с таймингом: https://vk.com/video-205546952_456241186?t=29m25s

Обратим внимание, что первые три операции в Python имеют свои обозначения. Импликация в Python не реализована как отдельная операция, но мы используем некий квазизаменитель, некий лайфхак, который ведет себя как импликация, это знак меньше-либо равно, то есть когда ставим знак «меньше или равно», выполняется импликация. Если проверить операцию сравнения «меньше» либо «равно», то мы получим результат соответствующий логической операции импликации.

Но так как это не логическая операция, а операция сравнения, её использование требует определенной аккуратности. Использовать такую замену просто так нельзя, необходимо проверять определенные условия. Эквиваленция, записывается тоже с помощью символа операции сравнения. И так же требует особого внимания при её использовании.

Рассмотрим в чём заключается особенность использования знаков операций сравнения в логических выражениях. Обычно в больших логических выражениях используются дополнительные скобки. Особенность заключается в порядке выполнения действий в выражении. Так, порядок действий в подобном логическом выражении должен быть следующим:

Запись этого выражения на языке Python будет выглядеть следующим образом

При этом, в первую очередь будет выполняться операция сравнения, т.к. таким образом реализованы приоритеты операций в Python. Следовательно, для корректной работы программы необходимо в выражении доставить скобки самостоятельно, согласно логическому приоритету.

На это необходимо обращать особое если в выражении используются операции импликации или эквиваленции.

Логические функции. Таблицы истинности

Ссылка на видео-разбор с таймингом: https://vk.com/video-205546952_456241186?t=41m30s

Логическая функция — это функция, в которой переменные принимают только два значения: логическая единица или логический ноль.

Рассмотрим пример типичной логической функции.

Логические функции исследуется с помощью таблиц истинности, в которых задаются все возможные значения переменных функции, и для каждой комбинации переменных вычисляется значение этой функции. Последовательно рассматривая все варианты значений переменных и подставляя их в логическое выражение, мы получим таблицу истинности:

Это аналитический способ получения таблицы истинности.

Для решения задач также можно строить таблицы истинности логических функций в Python.

Задача № 1 (53)

Логическая функция F задаётся выражением (¬x ∧ y ∧ z) ∨ (¬x ∧ ¬z). На рисунке приведён фрагмент таблицы истинности функции F, содержащий все наборы аргументов, при которых функция F истинна. Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных x, y, z.

В ответе напишите буквы x, y, z в том порядке, в котором идут соответствующие им столбцы (без разделителей).

Ссылка на видео-разбор с таймингом: https://vk.com/video-205546952_456241186?t=59m40s

Решение

В задаче дан фрагмент таблицы истинности из двух строк. В этих строках функция равна единице. Необходимо установить правильный порядок переменных в таблице. Первый шаг решения этой задачи — построение таблицы истинности данной функции. Полученную таблицу, в которой будут проставлены обозначения x, y, z, далее будем сравнивать с исходной таблицей, аналитически выделяя закономерности. Для этой задачи построим таблицу истинности аналитически. Рассмотрим, в каких случаях заданная функция будет равна 1 (т.к. в исходной таблице F=1). Т.к. выражение (¬x ∧ y ∧ z) ∨ (¬x ∧ ¬z) представляет собой логическую операцию дизъюнкция (сложение) двух скобок, значение 1 может быть в одной из скобок. Рассмотрим в качестве первого варианта первую скобку, значение 1 в этой скобке может быть в случае, если х равен 0, а z и у равны 1. Второй вариант равенство единице второй скобки. Вторая скобка будет равна 1, в случае, если х будет равен 0 и z будет равен 0. Т.к. «у» во второй скобке может быть любым запишем в нашу таблицу истинности оба варианта строк. Важным является то, что мы знаем, как в нашей таблице располагаются х, у, z. Сопоставим заданную и полученную нами таблицу.

Порядок строк и положение столбцов в заданной и полученной нами таблице может быть различными, но количество цифр нулей и единиц при правильном составлении таблицы совпадает, поэтому для решения задачи нам достаточно проанализировать количество нулей и единиц в столбцах и строках обеих таблиц. Обращаем внимание, что в столбце х, полученной таблицы располагаются три 0, и это единственный столбец с тремя нулями, следовательно, такое же расположение 0 должно быть и в заданной таблице, это второй столбец. Рассмотри столбец построенной таблицы с двумя единицами, это столбец у, и, значит, в исходной таблице это тоже будет столбец у. Оставшийся столбец получает значение z.

Получаем ответ zxy

Код построения таблицы истинности для проверки.

Ответ: zxy

Задача №2 (1617)

Логическая функция F задаётся выражением (x → y) ∧ (y → z).

На рисунке приведён фрагмент таблицы истинности функции F. Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных x, y, z.

Ссылка на видео-разбор с таймингом: https://vk.com/video-205546952_456241186?t=1h4m55s

Решение

Для решения этой задачи построим таблицу истинности с помощью программы.

Результат работы программы

x y z
0 0 0
0 0 1
0 1 1
1 1 1

Полученная таблица состоит из 4 строк. Обратим внимание, что строк в таблице, полученной программой больше, чем в исходной, такая ситуация является нормальной. Далее мы сопоставим полученный результат с исходной, приводя в соответствие строки, полученные программой, строкам заданной таблицы. Т.к. в исходной таблице отсутствуют строки с тремя нолями и тремя единицами, мы можем определить это соответствие. Далее, анализируя данные в оставшихся столбцах получаем, что х соответствует столбцам с двумя нулями, z — с двумя единицами, у будет располагаться в оставшемся столбце

Ответ: zyx

Задача № 3 (55)

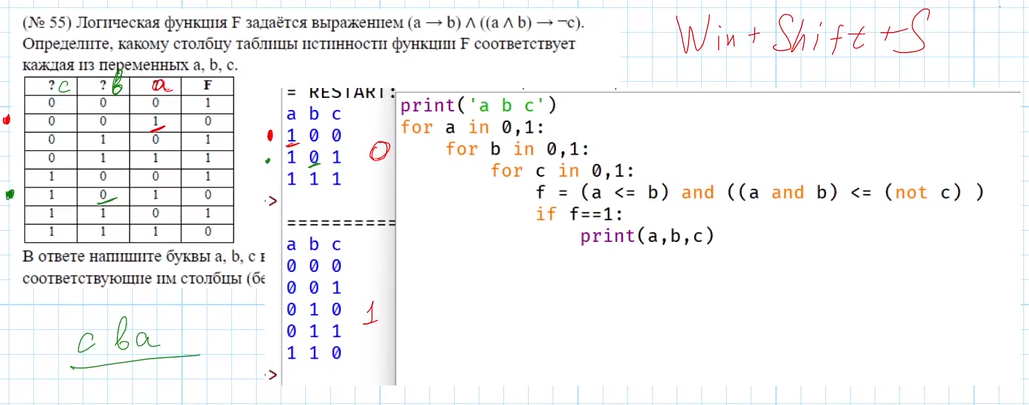
Логическая функция F задаётся выражением (a → b) ∧ ((a ∧ b) → ¬c). Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных a, b, c.

В ответе напишите буквы a, b, c в том порядке, в котором идут соответствующие им столбцы (без разделителей).

Ссылка на видео-разбор с таймингом: https://vk.com/video-205546952_456241186?t=1h10m5s

Решение

В условии этой задачи таблица полностью заполнена, но значения F идут не по порядку. Обратим внимание на то, что если для решения задачи требуется вывод полной таблицы всех значений, удобнее будет строки сгруппировать. Например, сначала вывести строки имеющие значение 1, а затем строки имеющие значение 0, и работать отдельно с каждой группой.

Последовательно запуская программу для f=0 и f=1, получим два соответствующих фрагмента таблицы истинности. Используя комбинацию клавиш Win +Shift + S, создадим скриншот с результатом работы программы и проанализируем полученные фрагменты таблицы. Выделим уникальным образом совпадающие строки полученной и исходной таблицы. Это будет строка с одной единицей для f=0. Обратим внимание, что единица в этой строке в полученной позиции стоит в «а», значит в исходной таблице, «а» в этой строке тоже должна быть единицей, следовательно, мы можем определить столбец «а». Анализ строки таблицы с двумя единицами при f=0 (это тоже единственная такая строка) показывает, что единственный ноль в этой строке соответствует b, следовательно, и в исходной таблице для b это тоже будет ноль и он находится в соответствующем ему втором столбце. Таким образом, буква «с» будет располагаться в первом столбце.

Ответ: сba

Задача № 4 (1636)

(№ 1636) Логическая функция F задаётся выражением (x ∨ y) ∧ ¬(y ≡ z) ∧ ¬w.

На рисунке приведён частично заполненный фрагмент таблицы истинности функции F, содержащий неповторяющиеся строки. Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных x, y, z, w.

Ссылка на видео-разбор с таймингом: https://vk.com/video-205546952_456241186?t=1h17m40s

Решение

Построим таблицу истинности для заданного выражения аналитически, вручную. Проанализируем все три части выражения соединенных конъюнкцией. Чтобы значение этого выражения было истинным (F=1), все его части должны быть истины, т.е. также иметь значение 1. Т.к. для w используется операция отрицания, все значения соответствующего столбца будут равны нулю. С учетом операции дизъюнкции, логического сложения запишем возможные варианты для х и у. Учитывая, что перед второй скобкой находится знак отрицания, а в скобке операция эквивалентности укажем для z значения обратные построчно значениям у.

Проверим полученную таблицу с помощью программы.

Сопоставляем исходную и полученную таблицу.

Т.к. в полученной таблице столбец, состоящий из трёх нулей принадлежит w, делаем вывод, что в исходной таблице это может быть только четвертый столбец, т.к. в остальных присутствуют единицы. Соотнесем столбец в полученной таблице с одной единицей с единственно возможным вариантом столбца в исходной таблице, это первый столбец, следовательно, это z. Для определения мест для х и у проанализируем строки полученной таблицы. Анализ показывает, что строка с одной единицей может совпадать только со второй строкой исходной таблицы. Единственная единица в этой строке соответствует столбцу у. Следовательно, оставшаяся позиция является х

Ответ: zyxw

Задача №5 (3470) (Е. Джобс)

Логическая функция F задаётся выражением (x ∧ (y ∨ ¬z) ∧ w) ≡ (x → ¬y ∧ z).

На рисунке приведён частично заполненный фрагмент таблицы истинности функции F, содержащий неповторяющиеся строки. Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных x, y, z, w.

Ссылка на видео-разбор с таймингом: https://vk.com/video-205546952_456241186?t=1h25m

Решение

Построим таблицу истинности для заданного выражения.

Полученная таблица истинности состоит из трёх строк. Сопоставляем исходную и полученную таблицу и получаем ответ.

Ответ: yxzw

Задание №6 (7533)

(ЕГЭ-2024) Логическая функция F задаётся выражением ¬(x → z) ˅ (y ≡ w) ˅ y. На рисунке приведён частично заполненный фрагмент таблицы истинности функции F, содержащий неповторяющиеся строки. Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных x, y, z, w.

В ответе напишите буквы x, y, z, w в том порядке, в котором идут соответствующие им столбцы. Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.

Ссылка на видео-разбор с таймингом: https://vk.com/video-205546952_456241186?t=1h28m45s

Решение

Построим таблицу истинности для заданного выражения.

Полученная таблица состоит из трех строк. Сопоставим ее с исходной таблицей. Анализируя таблицу, увидим, что столбец из трёх единиц может быть расположен только в четвертой позиции, следовательно, это буква w. Аналогично определим местоположение столбца из трёх нулей, соответствующих у, это третий столбец. Соотнесем строку таблицы с двумя единицами (она единственная в полученной таблице). Т.к. в этой строке одна из единиц является значением w, а вторая в полученной таблице принадлежит столбцу z, следовательно, в исходной таблице z может располагаться только в первом столбце, где также находится единица. Переменной х остается второй столбец.

Ответ: zxyw

Задание № 7 (6013)

(А. Богданов) Логическая функция F задаётся выражением ¬y ∧ (x ≡ (w → z)).

На рисунке приведён частично заполненный фрагмент таблицы истинности функции F, содержащий неповторяющиеся строки. Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных x, y, z, w.

В ответе напишите буквы x, y, z, w в том порядке, в котором идут соответствующие им столбцы. Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.

Ссылка на видео-разбор с таймингом: https://vk.com/video-205546952_456241186?t=1h35m

Решение

Обратим внимание, что таблица неоднородна. В ней есть две строки равные единице и одна равная нулю. Следовательно, при решении задачи мы должны будем рассматривать всю таблицу, состоящую из 16 строк, целиком

Построим таблицу истинности отдельно для значений функции равным нулю и отдельно для равных единице.

Для значения функции равных единице мы получим таблицу из 4-х строк, две из которых соответствуют заданной таблице. Для значений функции равных нулю получим таблицу из 12 строк, из которых одна соответствует заданной таблице. Т.к. полученные значения y все равны нулю мы можем точно определить его положение и это будет четвертый столбец (в остальных в значениях при f=1, у имеет одно из определенных значений также равных 1). Заметим, что в значении f=0 «у» тоже равен нулю. Следовательно, все строки из таблицы при f=0, где у=1 можно не рассматривать. Анализируя таблицу при f=1, определим, что строка, содержащая две единицы единственная, как и в исходной таблице. Следовательно, мы можем определить ее место. Увидим, что в этой строке значения нулей принадлежат y и w. Т.к. позиция у уже определена, мы можем определить позицию w во втором столбце таблицы. Т.к. w при f=0 тоже равна 0 мы можем соотнести эти строки таблиц. В строке полученной таблицы единица соответствует значению z, следовательно, мы можем определить её положение в исходной, заданной, таблице – третий столбец. Для значения х остаётся позиция в первом столбце.

Ответ: xwzy